2020. 3. 2. 21:23ㆍ알고리즘 문제풀기/자료구조
sparse table(스파스 테이블)이라고 불리는 기법이 있습니다. 이 기법에 대해 설명하는 글입니다.
예제를 통해 알아봅시다.

방향 그래프가 있습니다. 모든 점마다 나가는 화살표가 꼭 한 개씩 있습니다.
정점 하나에 말을 놓고, 이 말을 한 칸씩 움직일 거예요.
현재 있는 점에서 나가는 화살표가 한 개 있으니, 그걸 타고 새로운 점으로 갑니다.
새로운 점에서, 그 다음으로 갈 수 있는 곳도 하나밖에 없습니다. 나가는 화살표가 한 개니까요.
이렇게 나가는 화살표를 타고 계속 이동할 수 있습니다. 잘 생각해 보면, 무한히 여러 번 이동할 수 있습니다.
그렇다면 어떤 점 v에서 시작해, k번 전진했을 때 어디에 도착할까요? 이 질문에 빠르게 대답할 수 있을까요?
이런 그래프를 functional graph라고도 합니다.
이 문제에 functional graph의 성질을 이용한 별해도 있지만, 이 글에서는 sparse table을 이용해서 풀어보겠습니다.
각 정점에서 한 칸만큼 이동했을 때의 도착지점을 그림으로 나타내 보겠습니다.
사실, 안 나타내도 될 것 같아요. 위의 그림과 똑같을 것 아니겠어요? 생략하겠습니다.
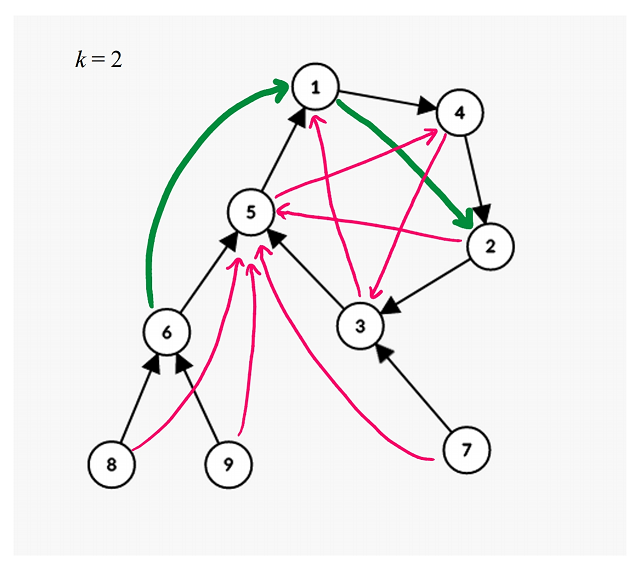
이제, 두 칸씩 이동했을 때의 도착지점을 봅니다.
복잡한 그림이 나왔습니다.
그림 자체에는 신경 쓰지 말고, 이제 k=2인 경우에 대해 바로 답을 말할 수 있게 되었습니다.
가령 "v=8에서 시작해 k=2만큼 가면 어디에 도착하는가"의 답은 "5에 도착한다."가 되겠죠.
8에서 시작해 8→6→5의 순서를 거치지 않고도 바로 알 수 있습니다.
그런데 누군가 k=4인 경우를 물어봤다고 합시다.
"v=6에서 시작해 k=4만큼 가면 어디에 도착하나요?"라고 물어왔을 때, 여러분은 어떻게 하실 건가요?
6에서 시작해 6→5→1→… 하며 다시 하나하나 갈 필요가 있을까요?
아니죠. 위의 그림에서 분홍색 화살표를 두 번 사용하면 됩니다.
아래 그림처럼요.
"v=6에서 k=4칸만큼 전진"하는 건, "v=6에서 k=2칸만큼 전진"한 정점에서 한 번 더 "k=2칸만큼 전진"한 것과 같으니까요. 답은 "2에 도착한다."입니다.
이제 우리는 k=2인 경우에 즉답을 할 수 있고, k=4인 경우에도 조금 생각하면 바로 답을 할 수 있게 되었습니다.
아니, 그냥 위의 그림을 사용해서, k=4인 경우의 그림을 새로 그릴 수도 있겠어요.
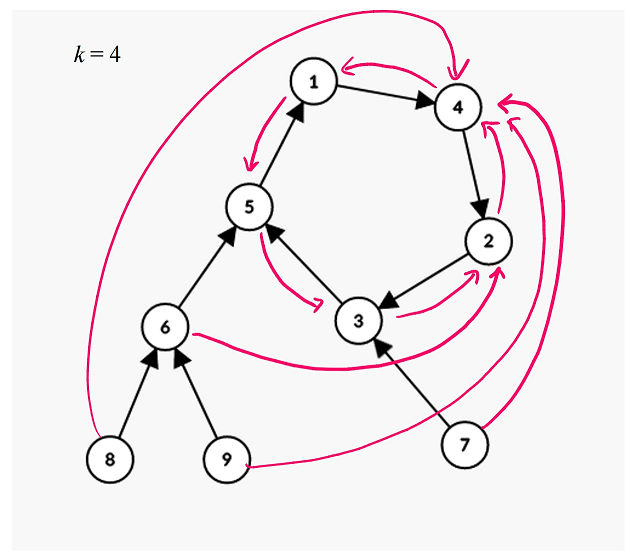
이제 이 그림만 있으면 k=4인 경우에도 즉답이 가능합니다. 뿌듯하네요…!
그런데 또 누군가 와서 예상치 못한 질문을 합니다.
"v=8에서 출발해 k=8만큼 가면 어떻게 되나요?"
아… 드디어 우리의 패배인가요? 8에서 시작해 8→6→1→… 이렇게 여덟 번을 가야 할까요?
아니죠, 이것 역시 위의 그림을 사용하면 금방 알 수 있답니다. 아래와 같이요.

v=8에서 k=4만큼 가면 4에 도착하는 걸 알고 있거든요.
다시 거기서 k=4칸만큼 가면 이제는 1에 도착하겠죠?
이제 k=4뿐만 아니라 k=8인 경우까지 척척 해결할 수 있습니다.
뿌듯해하고 있던 찰나… 마지막 질문이 우리를 급습합니다.
"v=7에서 k=7만큼 가면 어디로 가나요?"
어떡하죠? 지금까지 k=1, 2, 4인 경우에 쓸 그림만 그렸는데, 난데없이 k=7이라니요.
이제 정말 패배를 인정하고 7→3→5→… 이 단계를 일곱 번이나 거쳐야 할 때일까요?
사실은, 그렇지 않습니다. 위의 그림을 활용할 여지가 아직 남아 있습니다.
우선 7이라는 숫자를 가만 보면, 이렇게 쪼개집니다.
7=4+2+1
이제 감이 오시나요?
v=7에서 시작해서, k=4만큼 걸어가 보고,
다시 거기서 k=2만큼,
다시 거기서 k=1만큼을 걸어간다고 생각하면,
각각의 단계마다 위의 그림을 사용할 수 있습니다.
v=7, k=4인 경우 그림을 보면 도착지가 4라는 걸 알 수 있습니다.
이제 4를 출발지(v)로 삼아서, v=4, k=2인 경우의 그림을 봅니다. 이번에는 3에 도달하네요.
마지막으로 v=3, k=1인 경우는 그림의 검은색 화살표를 따라가면 5에 도착합니다.
따라서 도착점은 5입니다.
지루하게 일곱 번을 셀 필요가 없이, 그림을 세 번 쓰는 걸로 해결했네요!
이제 이 원리를 조금 더 구체적으로 설명합니다.
k에 따라, 출발점-도착점 관계를 표로 나타내면 이렇습니다. (위의 그림의 화살표를 숫자로 쓴 것뿐이에요)
| v | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | …에서 |
| k=1 | 4 | 3 | 5 | 2 | 1 | 5 | 3 | 6 | 6 | …에 도달 |
이제 k=2인 경우를, 이 표만 가지고 구해 볼까요?
| v | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | …에서 |
| k=1 | 4 | 3 | 5 | 2 | 1 | 5 | 3 | 6 | 6 | …에 도달 |
| k=2 | 2 | 5 | 1 | 3 | 4 | 1 | 5 | 5 | 5 | …에 도달 |
분홍색의 두 값을 통해서 녹색의 값을 알 수 있습니다.
k=4인 경우도, k=2의 줄만 써서 알 수 있습니다.
| v | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | …에서 |
| k=1 | 4 | 3 | 5 | 2 | 1 | 5 | 3 | 6 | 6 | …에 도달 |
| k=2 | 2 | 5 | 1 | 3 | 4 | 1 | 5 | 5 | 5 | …에 도달 |
| k=4 | 5 | 4 | 2 | 1 | 3 | 2 | 4 | 4 | 4 | …에 도달 |
처음의 그림에서 녹색 화살표로 표시한 부분을 위의 그림에 다시 한 번 나타내어 봤습니다.
이렇게 하면, k를 두 배씩 키워나가면서 각각의 k에 대한 답을 계산해돌 수 있습니다.
이제 k가 2의 거듭제곱 꼴인 경우에는 답을 구할 수 있고, 그렇지 않은 경우에도 어떻게 하면 되는지 대강 압니다.
코딩은 어떻게 할까요?
// 그래프가 nxt[1...N]에 주어져 있다고 가정.
// table[k][v]: v에서 k번 진행했을 때 도달하는 지점
int table[MAX_K+1][MAX_N+1];
// k=1인 경우 채우기
for (int i = 1; i <= N; ++i) {
table[1][i] = nxt[i];
}
// k>1인 경우, k를 두 배씩 키워가기
for (int k = 2; k <= MAX_K; k *= 2) {
for (int i = 1; i <= N; ++i) {
int tmp = table[k/2][i];
table[k][i] = table[k/2][tmp];
}
}말은 되는데, 사실 굉장히 웃긴 코드입니다. 이러면 table[3][...]같은 공간은 전혀 안 쓰거든요.
MAX_K를 백만 정도로 잡아도, 실제로 쓰는 공간은 20·MAX_V개의 int 뿐입니다.
그래서 보통은 table 정의를 이렇게 합니다.
// 그래프가 nxt[1...N]에 주어져 있다고 가정.
// table[k][v]: v에서 2^k번 진행했을 때 도달하는 지점
int table[MAX_LOG_K+1][MAX_N+1];
// k=0, 즉 한 칸 진행하는 경우 채우기
for (int i = 1; i <= N; ++i) {
table[0][i] = nxt[i];
}
// k>0인 경우, k를 1씩 키워가기
for (int k = 1; k <= MAX_LOG_K; ++k) {
for (int i = 1; i <= N; ++i) {
int tmp = table[k-1][i];
table[k][i] = table[k-1][tmp];
}
}이제, 주어진 문제를 어떻게 풀까요?
int solve(int v, int k)
{
int cur = v; // 현재 정점 위치
for (int i = MAX_LOG_K; 0 <= i; --i) {
if (k & (1 << i)) {
cur = table[i][cur]; // 2^i만큼 전진
}
}
return cur;
}
table의 계산(전처리)은 Θ(N·log(K))만큼의 시간/공간을 소요하고,
solve(v, k)의 문제 해결은 Θ(log(K))만큼의 시간을 소요합니다.
solve(v, k)의 문제 해결을 단순히 Θ(K)에 하던 것에 비하면 엄청난 차이입니다.
어째서 시간이 줄어들 수 있었을까요? 시간의 단축은 중복 계산의 제거로부터 (자주) 옵니다. 어떤 중복 계산이 빠졌을까요? 원리를 잘 생각해 보세요.
(여기는 고급 내용입니다.)
table의 구조에 대한 얘기가 조금 있습니다.
위에서 배열 인덱스를 [logK][N] 말고 [N][logK] 순서로 할 수도 있거든요. 그렇게 해도 당연히 잘 작동합니다. 같은 시간복잡도를 가지구요.
그런데, 이 sparse table에서는 위에 구현된 것처럼 [logK][N] 순서로 구현하면 훨씬 빨라요.
AC를 받을 만한 시간복잡도인데도, 순서를 반대로 했다가 TLE를 받는 경우도 굉장히 많습니다.
그 이유는 바로 CPU 캐싱 때문입니다. (캐싱은 복잡한 주제라서, 여기서는 대충 설명해 봅니다.)
위의 구현에서는 table[k-1][1...N]을 가지고 table[k][1...N]을 구하고 있는데, 이 두 배열은 각각이 메모리 상에서 연속하게 배치되어 있고(즉 table[k-1][2]의 바로 다음에 table[k-1][3]이 있습니다), 두 배열 사이의 거리도 멀지 않습니다.(table[k-1][MAX_N] 바로 다음에 table[k][0]이 있습니다.)
그래서 한 줄을 채우는 과정에서 접근하는 메모리 영역이 굉장히 좁고, 그 좁은 영역을 집중적으로 사용하게 됩니다.
예를 들어 MAX_N=200,000(=20만)인 경우를 보겠습니다.
앞쪽 줄의 크기가 781 KiB이고, 여기를 serial access 한 번+random access 한 번 합니다.
뒤쪽의 781 KiB짜리 줄은 심지어 완벽한 serial write입니다.
cache hit가 굉장히 많이 발생하겠죠. CPU를 완전 혼자 쓴다면 L2에도 들어갈 사이즈입니다.
반대로 table[1...N][k-1]을 가지고 table[1...N][k]를 구하는 경우를 생각해 봅니다.
(k-1)쪽 access는 stride가 (4 log(K)) bytes이고, working set은 Θ(N·log(K))짜리 배열 전체(!)인 read가 되겠습니다.
MAX_N=MAX_K=200,000(=20만)인 경우에, 이 정도면 random access와 다를 바가 없습니다...
random access는 working set 크기의 sqrt의 시간복잡도라고 주장하는 글(링크)을 생각해 보면, 배열 인덱스 하나를 반대로 썼다가 Ω(√N), 즉 Θ(√N) 이상의 시간복잡도를 떠안게 되는 셈이지요.
그리고 무엇보다, 인덱스를 반대로 쓴다고 해서 계산을 반대로 할 수는 없습니다. 바깥쪽 반복문은 항상 k여야 해요. (이유는 잘 생각해보면 알 수 있습니다.) 그러니 배열 인덱스도 가장 자연스러운 k-v 순서대로 적어주는 것이 좋겠습니다.
(여기까지가 고급 내용입니다.)
이것이 sparse table 기법입니다. sparse table 기법의 특징은 다음과 같습니다.
- 어떤 작업(예제에서는, 앞으로 한 칸 가기)을 여러 번 반복해야 할 때, 이를 빠르게 처리할 수 있게 해 줍니다.
- 하나의 값을 채우기 위해서, table을 두 번 연속으로 참조하는 과정이 들어갑니다.
- 정점이나 원소의 개수(N)뿐만 아니라, 반복할 횟수(K)가 시간·공간복잡도에 들어갑니다.
만약 이 K가 20, 30 하는 정도로 굉장히 작다면 sparse table의 크기도 굉장히 작아지고, 사실 쓸 필요가 없을 수도 있습니다.
반대로 K가 굉장히 커져서 2^64까지도 간다면 sparse table의 크기도 커집니다. "어차피 log를 붙이면 64배밖에 안 되는 거 아냐?" 하고 생각하실 지도 모르지만, N=500,000 (50만)인 경우에 (64·N)짜리 int 배열의 크기는 122 MiB나 됩니다. 메모리 제한이 빡빡하다면 어려울 지도 몰라요. - 기록 대상을 미리 알고 있어야 하며, 중간에 바뀌면 안 됩니다. 예를 들어 한 화살표가 바뀌면, 그로 인해 배열 전체를 갈아엎고 새로 계산해야 할 지도 모릅니다. 그러면 전처리(preprocessing)를 해놓은 의미가 없죠.
- 굉장히 다양한 응용이 가능합니다.
사용 가능한 작업은 "쌓을 수 있는 것"이면 다 됩니다.
k=4번 작업한 결과물 둘을 이어붙여서 k=8번 작업한 결과물이 되기만 하면 되지요.
예를 들어, 도착지점뿐만 아니라 그 지점까지 걸어가는 경로 상의 가장 작은 번호같은 것도 저장할 수 있습니다.
앞의 4걸음에서 본 가장 작은 번호,
뒤의 4걸음에서 본 가장 작은 번호가 있을 때, 단순히 둘 중 더 작은 것을 취하면 그게
전체 8걸음에서 본 가장 작은 번호가 되는 거니까요.
그럼 이걸로 sparse table을 하나 더 채울 수 있고,
"v에서 출발해 k번 걸어가는 동안 만나는 가장 작은 번호는?"과 같은 문제를 그대로 똑같이 풀 수 있어요.
이 문제를 풀지 못하면 여태껏 sparse table을 공부한 보람이 없습니다!! 조금이라도 고민해 보셨으면 좋겠습니다.
힌트. 가장 작은 번호만 가지고 있는 sparse table을 만들 때, 원래의 sparse table,
즉 목적지를 계산하는 table도 여전히 필요합니다.
(밑줄친 말은 허풍이고, 뒤가 본심입니다.)
배열에도 sparse table을 적용할 수 있습니다.
table[k][i]에, i번째 원소부터 연속한 2^k개에 대한 정보(예를 들어, 그 중에 제일 큰 것)를 기록해 보는 방식입니다.
이 경우 도착점에 해당하는 table은 구할 필요가 없습니다. (i+(1<<k))가 그 값인데요 뭘.
이 역시 그 정보가 합칠 수 있는 종류의 것이어야 합니다.
예를 들어 그 연속한 2^k개에 대해, (가장 작은 것을 제외한 나머지의 합)같은 걸 저장할 수는 없습니다.
위의 연산에 따르면 [1, 4]에서 5-1=4, 그리고 [3, 5]에서 8-3=5가 나오게 되지만,
4와 5만 가지고는 [1, 4, 3, 5]에서 13-1=12가 나올 것으로 추측할 수가 없다는 거죠.
이렇게 하면 질문에 대한 응답이 Θ(1)에 가능한 경우가 있어요.
예를 들어 최대값을 기록했다고 합시다.
이제 배열의 [3...9] 인덱스에 있는 값 중 최대값에 대한 질문이 들어왔습니다.
궁금한 구간의 너비가 총 7개 원소입니다. 이걸 너비 4짜리 구간 두 개로 덮는 아이디어가 있습니다.
즉 [3...6]과 [6...9]의 두 개 구간으로 겹치게 덮으면 구간 전체를 처리할 수 있게 됩니다.
따라서 k=2 (즉 2^k=4)인 행에서, i=3 및 i=6의 값을 가져와 max를 취하면 답을 알 수 있습니다.
물론, 가장 큰 2의 거듭제곱을 찾는 과정도 엄밀히 말하면 Θ(log K)이고,
겹치게 적용할 수 없는 연산(예를 들어, 구간의 합)의 경우에는 적용할 수 없는 방법입니다.
그렇지만 서로 겹치게 덮어서 처리한다는 아이디어 자체는 너무 재미있지요.
'알고리즘 문제풀기 > 자료구조' 카테고리의 다른 글
| 구간의 합 구하기 (0) | 2018.07.27 |
|---|---|
| Treap (0) | 2015.07.08 |
| Binary Indexed Tree와 구간의 사용방법 (0) | 2013.09.06 |
| Fenwick tree (0) | 2013.09.02 |